Introduzindo e implementando a função 'pdepe' - Problema de transferência de calor
Como já discutido na postagem que abordou teoricamente o assunto EDP, EDPs parabólicas são largamente encontradas em aplicações científicas de diversas áreas; e existe uma poderosa função interna do MATLAB® capaz de resolver esse tipo de equação diferencial: a função pdepe. Vejamos o seguinte problema:
Em uma situação de transferência de calor, uma placa de largura L é aquecida em um lado por uma superfície que possui uma fonte de calor (figura) e no outro lado a temperatura é fixa (T = 0ºC), como podemos observar na ilustração:
FIGURA 1: Ilustração do problema de EDP - Transferência de calor
Dessa forma, a placa tem uma temperatura inicial T = 0ºC e há um aumento de calor com o tempo da direita para a esquerda até que se chegue a um estado estacionário. A EDP que descreve o problema é:
onde k = condutividade térmica atômica da placa, ρ = densidade superficial da placa e Cp é o calor específico. As condições iniciais para a resolução do problema são:
i) Temperatura da placa em t = 0, T(x,0) = 0;
ii)
iii) Temperatura do lado direito da barra para todo t, T(L,t) = 0.
Assim, temos duas condições de fronteira e uma condição inicial (em t = 0). Assim, o problema é resolvível. Vamos agora entender os mecanismos da função residente pdepe e implementar a resolução do problema.
Função residente pdepe e implementação para o problema
A ferramenta consiste na resolução de uma equação geral padrão, que é a seguinte:
No lado esquerdo da equação, percebe-se a existência de uma função c dependente de x, t, u (temperatura) e ∂u/∂x; essa função é multiplicada pela derivada parcial em relação ao tempo ∂u/∂t. No lado direito da equação, temos as funções f e s. O termo m das expressões (x-m) e xm é 0 para coordenadas cartesianas, 2 para coordenadas cilíndricas e 3 para esféricas. No problema proposto, trabalharemos com coordenadas cartesianas, logo, m = 0.
Devemos inicialmente passar para o MATLAB as funções c, f, s, a condição inicial e as condições de contorno do problema. As últimas devem ser implementadas obedecendo o seguinte modelo:
Como temos duas condições de contorno, teremos dois modelos implementados. Tendo implementado todos esses parâmetros, a função residente resolverá a EDP que descreve o problema.
Para o problema estudado, é de fácil percepção que u = T, logo ∂u/∂t = ∂T/∂t e ∂T/∂x = ∂u/∂x. Fazendo uma breve comparação com a equação geral requerida pela função pdepe, observamos que:
O valor de f ficou dessa forma para que, quando multiplicado pelo termo ∂u/∂x resulte na equação inicial do problema. Como não temos nenhum outro termo, s = 0. Para as condições de contorno, comparando com o modelo estabelecido, temos:
Onde f foi definido anteriormente como k(∂T/∂x); x = 0, pois é o ponto da condição de contorno; p é o termo constante, igual a q''; q é o coeficiente de f, igual a 1. Na outra condição de contorno, temos:
Temos T(L,t) = 0 e não há dependência com ∂T/∂x, então q = 0; p = T; x = L pois é o local onde a condição foi estabelecida.
Agora resta realizar a implementação no MATLAB.
O programa foi dividido em 4 scripts, sendo o programa principal (executável) e três sub-rotinas: uma para a implementação dos parâmetros da equação geral da função pdepe, outro para a implementação da condição inicial (t = 0) e o último para a definição dos parâmetros do modelo da condição de contorno. Vejamos:
Sub-rotina 1: Implementando os parâmetros da equação geral
FIGURA 2: Sub-rotina 1
Sub-rotina 2: Implementando a condição inicial (em t = 0)
FIGURA 3: Sub-rotina 2
Sub-rotina 3: Implementando os parâmetros do modelo para as condições de contorno
FIGURA 4: Sub-rotina 3
Programa principal: Programa a ser executado
Este programa define as constantes e os parâmetros triviais, chama a resolução pela função residente pdepe e mostra os resultados em forma gráfica.
FIGURA 4: Programa principal
Os resultados gráficos obtidos foram os seguintes:
FIGURA 5: Gráfico da temperatura em função do tempo e da largura
FIGURA 6: Gráfico da temperatura em função do tempo
FIGURA 7: Gráfico da temperatura em função da largura
Sugestões:
Para maior aprofundamento acerca da função interna do MATLAB utilizada (pdepe), recomenda-se utilizar as funções doc ou help do software. Para tal, basta digitar doc pdepe ou help pdepe na janela de comandos e teclar Enter.
• Clique aqui para ter acesso aos códigos.
• Clique aqui para ter acesso aos códigos.
Referências:
CHAPRA, S. C.; CANALE, R. P.; Métodos Numéricos para Engenharia, Tradução da 5ª Edição, AMGH Editora Ltda., Porto Alegre, 2011;
CHAPRA, S. C.; Métodos Numéricos Aplicados com MATLAB® para Engenheiros e Cientistas; 3ª Edição, AMGH Editora Ltda, Porto Alegre, 2011;







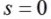












Comentários
Postar um comentário