Resolução de integral numérica – Método do trapézio composto

       Quando começamos a aprender integrais, a primeira noção, que equivale a uma integral é primitivar uma função. Porém a integral pode nos dar mais que uma primitiva de uma função, pode nos dar também valores relacionados a gráficos e figuras geométricas. 

         A ­­­integração aparece com freqüência na solução de problemas e no calculo de grandezas da engenharia e na ciência. Integrais e a operação de integração também são usadas na solução de equações diferenciais.

            A integração numérica baseia-se em estimar o numero de I(f) correspondente à integral de uma função f(x) entre os limites a e b. Porém quando temos um intervalo muito grande também teremos um erro muito grande associado a essa resolução. Mas para minimizar esses erros dividimos esse grande intervalo em pequenos intervalo fazendo a integral de cada subintervalos e somando-os.  Assim analisando uma representação de uma função no plano cartesiano, o valor da integral seria a área abaixo da função.

Figura 1: ilustração de uma integral definida

            Porém quando se tem experimento no qual temos apenas valores experimentais ou então a integração analítica é de difícil resolução, utilizamos então a integração numérica. A integração numérica utiliza vários métodos que facilita a resolução de problemas. Temos os métodos abertos e fechados.

            No método fechado, utiliza-se os pontos finais do intervalo na fórmula que estima o valor da integral. Os métodos que são considerados fechados são: o método trapezoidal e o método de Simpson. Já no método aberto esse intervalo de integração se estender além dos limites determinados, o método do ponto central e o método da quadratura de Gauss são considerados métodos abertos. Essa publicação tem como foco a explicação do método trapezoidal.

Método trapezoidal composto:

            Esse método consiste em resolver uma integral definida dividindo-a em varias partições. Partindo desse pré-suposto temos então que, uma integral definida no intervalo de a até b, dividimos ela em N subintervalos com a definição dos pontos x1, x2, x3, x4, ..., xN+1. Onde x1=a e xN+1=b. Para obter N intervalos tem que ter N+1 pontos.

           

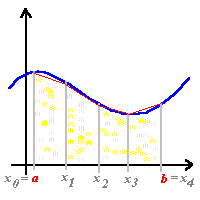
Figura 2: Divisão de N intervalos para o método do trapézio composto.

            Tomando com base a figura 2 tem que, é uma função limitada pelo intervalo [a, b], onde a=x0 e b=x4. Nota-se que, esse intervalo foi dividido em 5 pontos formando assim 4 subintervalos.

            A integral então será:

Nota-se que cada subintervalo pode ser visualizado como um trapézio. A área de um trapézio é dada por [Base(maior)+Base(menor)*h]/2. Considerando que h=(x1-x0) e as Bases= f(x0) e f(x1). A integral do subintervalo [x0,x1] é dada por [(f(x0)+f(x1))/2]*[x1-x0].

            Analisando o conjunto de integrais (1) pode-se então reescrever como sendo:

            A equação (2) é a fórmula geral para o método trapezoidal composto. Para esse caso não necessariamente os subintervalos devem ser de espaçamentos idênticos. Porém quando se tem subintervalos com espaçamentos idênticos a equação (2) pode ser simplificada para:

                                 

              Para trabalhar com esse método no MATLAB, o ideal será criar uma sub-rotina, a qual tem como finalidade facilitar a montagem do programa que se quer utilizar.

            Usando o MATLAB para resolução de integral pelo método do trapézio composto temos que fazer primeiro uma sub-rotina, a qual esta a parte que irá fazer os cálculos.

function I = trapezio(f,a,b,n)

h =(b-a)/n; % determina o incremento para n subintervalos

x=a; % define o primeiro ponto

y=eval(f); % avalia a função para o primeiro ponto

I = h/2 * y; % inicializa a soma para o primeiro ponto

for i=1:(n-1); % para os restantes pontos até n-1:

 x = a + h*i; % calcula o ponto seguinte

 y = eval(f); % avalia a função neste ponto

 I = I + h*y; % incrementa a soma

end

x=b; % define o último ponto

y=eval(f); % avalia a função para o último ponto

I =I + h/2 * y; % adiciona o último termo à soma

Depois de ter feito a sub-rotina:

%esse programa tem como objetivo resolver integrais

%a partir do metodo do trapezio usando a sub-rotina trapezio

fun=input('Introduza a função (como string): '); %comando para introduzir

%a função

disp('Introduza o intervalo para x:'); %comando para adcionar os intervalos

a=input('a='); b=input('b='); %adicionar os intervalos a e b

n=input('Introduza o número de subintervalos: '); %adicionar a quantidade de subintervalo N

I=trapezio(fun,a,b,n);

disp('O valor aproximado da integral: '), disp(I);

            Pronto, o programa está pronto. Basta rodar e introduzir as informações na tela de comando que obterá o valor aproximado da função integrada em determinado intervalo. 

Clique aqui para ter acesso aos códigos!